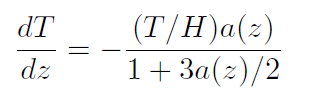The discussion concerning the temperature profile of an ideal gas under the force of gravity has a long
history. There are many excellent
texts on this subject so I will mostly refer the reader to these and just add a few comments of my own.
In an old book on the history of statistical mechanics entitled "The kind of motion we call heat" you can find the following passage:
"...According to Herapath, the force of gravity by itself produces a temperature variation in a vertical column of air, namely a decrease of about 1 F for every 100 yards increase in height above the earth's surface (assuming perfectly dry air); the 'total altitude of the air' would thus be approximately 31 miles, if it terminates when the temperature has dropped to absolute zero.
Herapath's work was refused publication by the Royal Society of London but seems to have had ample publicity through its appearance in several issues of the Annals of Philosophy...."
Clearly,
if Herapath is right then the greenhouse hypothesis is wrong, as is explained in the post
"What is the greenhouse effect". But is Herapath right? Well, the Royal Society seemed skeptical at the time. There is one problem with his hypothesis that can be expressed quite simply:
The temperature must not become negative
This is so obvious so why do I mention it? Well, if we assume that the ground temperature of the earth is on average 288 K and that the temperature decreases by 9.8 degrees C per kilometer, then the atmosphere must "end" at an altitude of approximately 30 km, otherwise the temperature will become negative. Today we know that the atmosphere extends to much higher altitudes and that the temperature appears to be stratisfied beginning already at an altitude of 11 km. The stratification must occur at some point independent of any ozone absoption of UV-light and so on.
However, there seems to be something intuitively appealing with the assumption that temperature decreases with height independent of any motions or stirring of the air. In 1985 Coombes and Laue published a paper called "A paradox concerning the temperature distribution of a gas in a gravitational field":
Clearly, we must distinguish between the single particle kinetic energy expectation value and the
ensemble average. The fact that the particles with low energy must reside at lower altitudes means that they contribute to lowering the ensemble average of the kinetic energy at these altitudes. Or put in other words, the density decreases according to the barometric formula just as the pressure does, so if the ideal gas law is to be valid the temperature must be uniform in the column.
The problem can also be treated within the context of fluid mechanics under Navier-Stokes equations, yielding some similar but also some slightly different
answers.
So where do we go from here, what is the significance of the Coombes-Laue conclusion? We could make an attempt to analyze it from a logical point of view in the following way. Consider the following three definitions of temperature:
1. Absolute Temperature, denoted T
The absolute temperature could be defined using the notion of equilibrium in the following way: Whenever two systems in thermal contact with each other but isolated from the surroundings cease to exchange net heat (energy) they share some common property called temperature. The absolute temperature can be given a number according to the formula 1/T = dS/dE where S is the entropy and E is the internal energy. In order to define the entropy we need to identify the degrees of freedom of the system.
2. Kinetic Temperature, denoted T'
The kinetic temperature we define as the ensemble average of the translational kinetic energy of the molecules. This can only be applied to gases but is not excluded to ideal gases. Allowing the inclusion of water vapour and other gases with extra degrees of freedom does not pose any difficulties.
3. Empirical Temperature, denoted T''
The empirical temperature we define as the reading of some preferred thermometer. This definition differs from the others since it concerns the physical world and not "the world of ideas".
So, what Coombes and Laue showed, as well as many people before them, was that for a particular statistical ensemble, namely the canonical ensemble of an ideal gas in a gravitational field, we have that
T = T'. However, as a matter of fact this is no longer true if you consider the
microcanonical ensemble, though the difference in this case may be considered as rather insignificant. In any case, the more relevant question would be the following:
Is, under all circumstances, T = T' = T'' ?
It seems as if the greenhouse hypothesis implies the following answer to the above question:
Under all circumstances we have that
T' = T'', but
T = T' = T'' holds only if there are no greenhouse gases around. This of course requires that we treat the incoming sunlight as a heat flow regardless of the composition of the atmosphere. It appears as if the controversy concerning the greenhouse effect in relation to the
second law of thermodynamics can be formulated as a logical/semantic disagreement of the kind just described.
There are many interesting perceptions of the related problem concerning the atmosphere. The following passage was quoted in the
falsification paper of Gerlich and Tscheuschner:
"Some have problems with the energy that is radiated by the greenhouse gases
towards the surface of the Earth (150W=m2 - as shown above) because this energy
flows from a colder body (approx. -40 deg C) to a warmer one (Earth's ground approx.
+15 deg C) apparently violating the second law of thermodynamics. This is
a wrong interpretation, since it ignores the radiation of the Sun (even 6000 K).
With respect to the total balance the second law is obeyed indeed."
There is something very strange about this statement since if we follow the advice given and treat the incoming sunlight as a heat flow then there is no net heat flow between the surface and the atmosphere averaged over a day-night cycle.