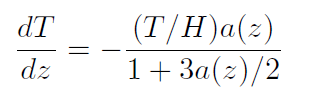What is the Greenhouse Effect, part 2

Having scrolled through G&Y's "Atmospheric Radiation" some more times, I thought it might be time to peel of another layer of the theory, which is somewhat related to my most recent posts. The key chapters I think are Chapter 2: "Theory of radiative transfer" and Chapter 9: "Atmospheres in radiative equilibrium".

Chapter 2 contains a long and complicated discussion about radiative transfer, that, after the dust is cleared (ie Taylor expansion to first order), I believe boils down to the following relation (using a slightly different notation):

B(a(z)) = sigma*T^4/pi   (1)

The right hand side is simply S-B's law divided by pi, and the left hand side is a source function, derived from a mish-mash of other considerations, whose main property I guess is that it increses with the optical parameter a(z). To a first approximation:

B(a(z)) = F(1 + 3a(z)/2)/(2*pi)   (2)

I guess the line of reasoning is something like this: The radiation must be a function of the heat source F and some optical absorption/emission coefficient a(z), but since the radiation must also equal the radiation given by S-B's law we now have a relationship between the parameters F and a(z) on the one hand and the temperature T on the other. 

Assuming also that a(z) is altitude dependent: a(z) = a*exp(-z/H), probably reflecting the fact that the density decreses roughly like that, we now have a relation between the temperature T, the altitude z and a. Differentiating both sides of equation (1) yields after some manipulation:

-dT/dz = (T/H)a(z)/(1 + 3a(z)/2)    (3)

Hence, we arrive at a lapse rate that depends explicitly neither on the heat source F nor the atmospheric mass, but instead solely on the optical parameter a(z). The heat source F is instead reintroduced in a rather ad-hoc fashion when fixing the ground temperature. This is peculiar. Furthermore, there is something odd about the assumption on the S-B law. Wouldn't it be more reasonable to assume that

Total radiation = F(a(z), T) ,

Where F is a function dependent on both the temperature and a(z).

A model should not be dismissed just because it is simplistic. However, when studying these equations and comparing them with the equally simplistic formulas that can be derived from conventional thermodynamics there is reason to raise your eye-brows.

G&Y themselves write the following about radiative equilibrium considerations:

"In addition to their value in examining general principles, there is a recurrent, although disputed theme that radiative equilibrium has direct relevance to the observed atmospheric structure"

This was in 1989. Twenty years later, "although disputed" has suddenly turned into "widely acknowledged", at least according to Saint Lindzen. So what happened in the mean time? Well, probably not any major educational effort on the part of established climatology, since very few people seem to know anything in particular about these matters.

The heat equation with energy source

We now continue to discuss the heat equation with an energy source. As an illustrative example we consider a rod with length L which is heated by an energy source E at position x = 0 and is maintained at a constant temperature T = 0 at position x = L by some external reservoir. The heat equation inside the rod reads

dU/dT = D*d^2U/dx^2

The reservoir is incorporated as the boundary condition:

U(L) = 0

In order to determine the appropriate boundary condition at position x = 0 we temporarily switch to a discretized mesh in the position coordinate with steplength 1:

Rate of change of energy per unit time = Heat gained by energy source per unit time - Heat lost to adjacent position per unit time

dU(0)/dt = E - D(U(0) - U(1))

Which in the continuum limit becomes:

dU(0)/dt = E + D*dU(0)/dx

As before we now ask for the stationary solution, that is the solution for which dU/dt = 0 everwhere. Inside the rod we have

D*d^2U/dx^2 = 0

with solution U(x) = Bx + C, which without the boundary conditions would  be independent of the diffusivity constant D. Taking into account the boundary condition we arrive at the solution

U(x) =  E/D*(L - x)

And in particular U(0) = E*L/D, which decreases as the diffusivity constant increases.

This could now maybe serve as the first babystep towards a heat equation for our atmosphere (which must also in the end incorprate convection etc etc) if the energy source is reinterpreted as the incoming sunlight. But there is a slight complication here. The incoming sunligt must pass through the upper atmosphere before it reaches the surface of the earth. Is this just "incidental", or would it perhaps be appropriate to include the incoming sunlight as simply a component of the total energy U(x). In that case the model system would be in equilibrium with a constant temperature. So which is the way to go? Well, I myself is not sure about this, but maybe you have some suggestion?...

The heat equation revisited

Let's recall the heat equation in one spatial dimension:

dU/dt = D*d^2U/dx^2

Here U is the heat-content or temperature at a given position and time, and D is the diffussivity constant. In order to completely solve the heat equation one needs to specify boundary conditions which might depend on various energy sources et.c., but we will not be so much concerned with that here. Often one is interested in finding a stationary solution that does not change in time, and for such a solution we have that dU/dt = 0 everywhere. The stationary one-dimensional heat equation is thus D*d^2U/dx^2 = 0.

Now let's try to construct a simple radiation model for an almost ideal gas. Many of the thermodynamic properties of an ideal gas, such as the energy content and pressure, are proportional to temperature so let's assume that we can interchangeably speak about the heat content and temperature. Suppose that the radiation is proportional to the temperature U and also proportional to a parameter A which is a measure of the emmisivity. Let's discretize the position variable with an index n. To start with, also suppose that every layer absorbs all incoming radiation (an unphysical assumption that we will later relax). If we now try to find a stationary solution, that is a solution that does not change in time, then there is no build-up or loss of energy and hence we must have balance between incoming and outgoing radiation. Now take the perspective of the layer at position n

In words:

Heat absorbed from the adjacent layers - Heat lost by radiation = 0

In numbers:

AU(n-1) + AU(n+1) - 2AU(n) = 0

Notice in particular the "back-radiation" term AU(n+1). However, what we have just written is simply the discrete form of the stationary heat equation:

A*d^2U/dx^2 = 0,

now with the diffusivity constant simply given by the emissivity parameter A. Relaxing the assumption that all incoming radiation is absorbed leads in its simplest form to the model I described in the post "A simple radiation model". One can of course take into account all sorts of other circumstances, for example a position dependent thickness of the gas and so on, but very quicly such more elaborate models become analytically intractable and one would probably need to use computers. 

However, the main message is that a model which incorporates "back-radiation" does not necessarily lead to a greenhouse effect.

A comment on Claes' answer to Roy

In a recent post Claes Johnson attempts to answer the following question from Roy Spencer:

How does the surface 'know' how opaque the atmosphere is before it 'decides' at what rate it should emit IR?

There is one point which I would like to make here which seem to have escaped many GHE-skeptics. In a previous post I constructed a simple radiation model, which does not necessarily come close to the real situation, but which nevertheless highlights something important. In the model in question no part of the system 'knows' what goes on anywhere else, the only things each part knows is its own temperature and absorptivity. The model also contains 'backradiation'. Moreover, the 'backradiation' taken alone does in fact slow down the rate of cooling in the system. The question is now: Does the model reproduce anything like the greenhouse effect? The answer is: It doesn't. In the model the temperature lapse rate flattens as the absorptivity/emmisivity increases with the consequence that the system cools, which is a clear deviation from the so called GHE.

The reason for this is probably the following: The amount of backradition can never exceed the radiation that at the same time is lost to outer space. Thus the backradiation cannot trap energy in the system since it is always associated with an 'out-radiation' that is equally big. 

The real difference with the GHE and reality is thus probably much more subtle than both Roy and Claes wants it to appear. To be honest, I have not quite understood the supposed mechanism of GHE although I have tried, but maybe I will succeed in the future to completely disentagle the mathematical structure of it. I very much encourage the mathematically inclined audience to also make such an attempt, since the present 'wordy' discussion on 'backradition' has not managed to clear the confusion. 

My suspicion though is that the greenhouse effect is based on a mechanism of reflection rather than absorption-thermalization-thermal reemission. Hence it is formally more akin to radiation pressure, but that remains to be clarified. Good luck.

Cloud or No Cloud

Much confusion surrounding the debate concerning the fundamentals of the greehouse theory, in my opinion can often be traced back to a careless hopping between concepts from equilibrium- and non equilibrium thermodynamics respectively. Here I will present a simple thought experiment that might highlight this issue. Consider a body which by regulated inner chemical reactions maintains a temperature of 37 degrees Celsius. Now consider two situations:

1. The body is placed in vacuum (outer space)

2. The body is surrounded by a nitrogen cloud which has a temperature of 20 degrees Celsius.

In case 1 it is obvious that the body will radiate energy to space at a rate which depends on its temperature. The exact law governing the magnitude of this radiation is not really important here, but let's suppose that it follows a T^4 law. But what about case 2? It seems obvious that the body will transport heat to the gas due to the temperature difference but how much will it radiate? Greenhouse theory given an unequivocal answer to that: It will still radiate as much as it did in vacuum, and since there are no greenhouse gases around there will be no back-radiation. In case 2 we are thus left with the conclusion that the body loses more heat to the surrounding than it did in case 1. But does this really make sense? I can think of several ways to argue that the body will in fact not radiate nearly as much as it did in vacuum, and I will for the moment leave it to the reader to think about this. If, however, you believe that the surrounding gas will reduce the amount of radiation it does have implications for the greenhouse effect, it means that the application of an equilibrium radiation law, like the Stefan-Boltzmann law, to a surface which is not equilibrated to the surrounding gas (with or without greenhouse gases) is invalid.

If you are still hesitant I might just through out the question quite bluntly:

Which would you like to try, cloud or no cloud?

Equilibrium contra Non-Equilibrium

In order to properly understand some of the aspects of the greenhouse debate, it is important to make clear the concept of equilibrium contra non-equilibrium. No real world system is ever in equilibrium, there are always disturbances. In the case of the earth these disturbances are, among many others, the rotation of the earth, the non-uniformly distributed sunlight, the moon, etc etc. So why do we use the concept of equilibrium at all. The way I see it is that the equilibrium is the imaginary state that the system strives towards but never reaches. And in order no know how the non-equilibrium state evolves we need to know its ultimate goal. If there is a temperature gradient, the system will strive to erradicate it as fast as it can. Or will it?...

Let's make things simple for a while. Let's take away all non-uniformities that create disturbances in the earth's thermodynamic system. No rotation, uniform sunlight, uniform oceans, no poles, no equator, no moon. What would it be like? The greenhouse hypothesis says that this system would be in equilibrium, but the equilibrium would be profoundly affected by the amount of greenhouse gases present in the system. The fact that things will be slighty different with a change of composition of the atmosphere is of no surprise, but the strange thing is that GHEH implies that this equilibrium would be characterized by a temperature gradient (or a "radiative-convective equilibrium") and that this temperature gradient can be considered caused by the greenhouse gases. Strange isn't it, an equilibrium with a temperature gradient, like a refrigerator working without electricity. But hey, so what, the real world atmospheric temperature gradient is indisputable. Or maybe it isn't?..

GHE proponents have of course developed a cunning way to get out of this dilemma. They argue that an equilibrium with a temperature gradient is not a violation of the 2nd law, since the earth is not in equilibrium anyway. Wicked isn't it :)

But let's not argue about that now. What do the skeptics say? Some skeptics say that this equilibrium which I sketched on before will indeed be characterized by a temperature gradient but it will be caused by gravity. Since the total energy of each molecule follows a Boltzmann distribution the molecules at higher altitudes will be slower than those at lower altitudes giving rise to a temperature gradient. Convincing isn't it? The only problem is that it is wrong, as was shown long ago. Given the assumptions, gravity doesn't cause a non-uniform temperature, instead it creates a non-uniform chemical potential. To make things even more complicated (and interesting) the chemical potential is temperature dependent. (Check out the previous post "On the temprature distribution of an ideal gas under the force of gravity"). This cannot be dismissed easily since even under the Navier-Stokes approach to fluid mechanics, the isothermal air parcel is a very stable and physical concept that can be extended to an infinite space domain.

There is however another aproach. One could claim that there is an atmospheric lapse rate because the earth is not in equilibrium and thats that. At the moment, Claes Johnsson and I discuss the consequences of this assumption. In this case the incoming sunlight is treated as an energy source heating the surface and the important question becomes how the thermal transport properties are affected by an increase in the optical activity of the atmosphere, characterized by a absorption/emission parameter A. Does an increase in A lead to larger radiative heat transport and flatter lapse rate or does it lead to increased isolation and a steeper lapse rate. The first corresponds to cooling, the latter to warming. A simple observation could give a hint to the answer to that question, consider two bodies with temperatures T1 and T2 that radiate against each other with an intensity AT^4. The net heat transfer is thus

 dQ = A(T1^4 - T2^4)

The heat transfer increases as we increase A, or what is your opinion? The thriller continues...

Folklores in Physics

When I did dimploma work in mathematics, on one occasion my supervisor said to me: "In mathematics and science there are things called folklores". What he referred to in his field was the existence of theorems that everyone went around believing that someone had proved but which in reality nobody had ever proved. We are  not talking about grand famous conjectures like the Riemann hypothesis but typically minor theorems in some new emerging field. In particular he remembered a conference where somebody, lets call him Y, went before the audience and announced that he was going to prove Theorem X and almost everyone in the audience started laughing. Theorem X was a folklore, but only Y knew about it.

During recent years I think I have discovered a folklore in Physics. I'm not talking about the Greenhouse Effect, physicists don't know anything about that, and besides, it is not really the kind of folklore we are discussing here. I'm talking about the folklore about the atmospheric temperature lapse rate. Almost every physicist, chemist, (and zoologist) think that it is simple and was solved long ago. Or put in other words: Nowadays every Tom, Dick and Harry thinks that somebody else knows how to derive it, but they are wrong. 

If you ask a physicist, if you get any answer at all he or she will probably say that it follows from fundamental gas laws. If pushed on the details about which of the infinite number of lapse rates you can derive from the fundamental gas laws he or she will probably say, look in the litterature, Gibbs must have solved it. But Gibbs never solved it, and neither did anyone else. The problem was discussed intensively long ago, but was forgotten and left unsolved by physicists. This void was then filled with the Greenhouse Effect, but they never told us about it...

The photon gas versus the ideal gas, round 2

As a warmup I thought we could have a look at the following paradoxical behaviour of two reservoirs of ideal gas put in a gravity field and allowed to exchange both energy and matter:

The yellow numbers indicate the kinetic energy of the molecules and the "temperature" standing to the right is simply the ensemble average of the kinetic energy. Now imagine that one of the molecules in the upper reservoir jumps down:

Taking into account that the molecule gains some kinetic energy during the fall we arrive at:

Look what happened! Energy went from lower temperature to higher temperature, thereby equating the temperature of both reservoirs. Pretty queer, huh. But if something is screwing things up here it is certainly not greenhouse gases. In a way this illustrates an important difference between the photon gas and the ideal gas concerning the relationship between internal energy and temperature:

As we can see, for the photon gas the internal energy density is simply a constant times the temperature to the power of four, period. For the ideal gas the situation is different:

Notice the "n", which is the particle density. Hence, in contrast to the photon gas, the ideal gas can have an arbitrarily nonuniform distribution of energy but at the same time be isothermal. Of course this is of no concern for climate science since in their world the atmosphere is a photon gas and an ideal gas at the same time. That is also pretty queer.

Misuses of the complexity argument

In many discussions you encounter the argument "the climate is too complex to be properly understood". But what does it really mean and why do people use it. I think that in many cases it is used to avoid some uncomfortable or difficult question. The more interesting question would be: "What aspects of climate are too complex to be properly understood". Let me give a few examples:

1. Why is it brighter during daytime than during night? Is that complex or simple?

2. Why is it warmer during summer than during winter? Is that complex or simple?

3. Why is the average temperature lower at 5 km altitude than at the surface? Is that complex or simple?

The last question has apparently shown to be too complex for physicists, but maybe it is in fact simple, that we are just too stupid to realize it? Who knows. Maybe the difficulty lies in the fact that the third question posed can under certain circumstances turn almost meaningless. Below I will give two examples of common usage of the complexity argument, one good and one bad.

1. Climatologists claim that the climate is largely determined by the greenhouse effect. They try to prove this hypothesis by running computer simulations and compare them with temperature records of the past, but in reality small temperature variations are too complex to model so the greenhouse hypothesis is still unproven.

2. Nobody has denied the greenhouse effect, but we don't know its future magnitude because climate is so complex. It can be plus 1 or plus 4 or maybe plus 100 degrees or perhaps even -1, who knows, climate is so complex so we shouldn't do anything anyway.

Which one of the above do you think is best?

Can Newton's third law say anything important about the atmosphere?

Here I will expand a little bit on the previous post "Why is something possible in Climate Science that is impossible in Nature?". I thought the most convenient form would be an interview with myself.

A: First question: How is it possible for a spacecraft to leave the earth?

A: It is because of Newton's third law. By spitting out mass and radiation in the downward direction the spacecraft must take the recoil, that is, a force of equal magnitude but with opposite direction. When this force overcomes the gravitational force Mg, where M is the mass of the spacecraft and g the gravitational acceleration the spacecraft leaves the earth. If the recoil is less than Mg after it has left the earth it will fall back again. If you have equality, it will hoover in the air.

A:  So you mean that radiation is a force?

A: Not exactly but almost, radiation carries both momentum and energy. A reformulation of Newton's third law is the law of conservation of momentum. Energy relates to force by the formula E = Fd where d is displacement. Laser is often used nowadays to move small objects.

A:  And when light is absorbed it is converted into heat?

A: Not necessarily, you could say that when it is absorbed it acts as a force, doing work on the absorbing material, and this work can then be dissipated into heat. But dissipation requires an environment.

A: Are you implying that this has importance to climate science.

A: Yes.

A: In what way?

A: For example, Erren and Dietze say the following: "..the Greenhouse effect (GE) is a radiative effect, i.e. warming from back-radiation to ground, which is independent of atmospheric mass.. and thus cannot be governed in its magnitude". That is clearly wrong, just look at the spacecraft. The atmosphere would fly away if the radiation exceeded a certain value.

A: Aren't you beeing somewhat ridiculous right now?

A: A little bit maybe, but we havn't come to my main point yet.

A: What is that?

A: Have a look at the image below, it depicts an air parcel in hydrostatic equilibrium. My point is that for a hoovering air parcel the amount of backspitting of momentum is precisely governed by its mass times gravity, just like the hoovering spacecraft. This momentum can be transferred either by direct molecular collisions or by backradiation, but they must add up to Mg for the parcel to be in mechanical equilibrium.

A: And your point is that the precise nature of this backspitting of momentum is unimportant for the heating impact of an atmosphere?

A: Precisely!

A: Have you talked with anyone else about this?

A: I've tried to.

A: Any results?

A: I don't know, but it seems as if most people prefer to use more advanced laws, such as conservation of energy, molecular spectra, HITRAN and so on. They probably think that Newton's third law is soo 17th century.

A: Ok, thanks for the interview.

A: My pleasure.

A Note: Newton's third law of course also applies to an oscillating force in the horizontal direction.

The Hypothesis of Claes Johnsson and the Rebuttal by Lennart Bengtsson

The story about Claes Johnsson's course litterature Body & Soul and the following media hype is comprehensively covered on his blog. The draft version of his book contained parts discussing atmospheric physics, but these were never included in the numerics course in which the book was used. Nevertheless, Lennart Bengtsson, swedish professor of meteorology at the University of Reading, found himself forced to give a rebuttal in the swedish newspaper Ny Teknik. Bengtsson's attitude towards the IPCC could be described as that he is a little bit for it, but also a little bit against it, whatever suits the circumstances. On the book by Claes Johnsson he is more categorical as you will see. Parts of Bengtssons newspaper article will be quoted, which I will translate to english to the best of my ability.


"..De avsnitt jag inspekterat är förfärande i sin fullständiga brist på relevant atmosfärkunskap. Jag skulle snarare vilja kalla det anti-kunskap.

Kap. 13 försöker på ett märkligt sätt att visa vad temperaturen! är vid atmosfärens övre gräns. Jag kan nämna att tropopausens temperatur ligger mellan -60°C och -80°C och knappast 0. Det man givetvis måste använda är den strålning/ytenhet som träffar atmosfärens övre gräns. Detta kan lätt beräknas och uppgår i årligt medelvärde för hela jorden till just 1/4 av solarkonstanten eller 341W/m2. 102 W/m2 reflekteras (planetärt albedo är 30%). Resten, 239W/m2, återstrålas mot rymden som långvågig strålning. Det inses lätt att den REPRESENTATIVA temperaturen för denna återstrålning är ca 255 K eller -18°C. Detta beror på att strålningen från jordytan absorberas av växthusgaserna som i sin tur strålar vidare från en lägre temperatur osv. Resonemanget i detta kapitel är totalt felaktigt. Vad som händer vid en ökad koncentration av växthusgaser är att den representativa utstrålningen sker från en högre nivå i atmosfären varvid konsekvensen blir en ytterligare förhöjd marktemperatur. Här är det bara att följa den fukt/torradiabatiska temperaturprofilen.....

....Hela det sk strålningsavsnittet vittnar om en total brist på insikt i mekanismerna för atmosfärisk strålning. Det ytterst omfattande arbete som pågått här under de senaste 50-75 åren beaktas överhuvudtaget inte. Författarna borde ta och läsa igenom Richard Goodys senaste utgåva från 1995 tillsammans med Y. L.Yung eller Kuo-Nan Lious bok från 2002. Det är mig en obegriplighet att dylikt nonsens kan skrivas från anställda vid ett av Sveriges främsta lärosäten, åtminstone gällde detta tidigare. Man kunde åtminstone konsulterat någon av de svenska professorerna i meteorologi eller någon utländsk expert på atmosfärstrålning för att undvika de allra värsta tokigheterna. Man kan bara hoppas att eleverna var intelligenta nog för att genomskåda rappakaljan som dessutom presenteras på ett beschäftigt och mästrande sätt...."

Which could be translated as:

"..The chapters I have inspected are appalling in their complete lack of relevant atmospheric physics. I would rather call it anti-knowledge.

In Chapter 13 there is a strange attempt to derive the temperature at the top of the atmosphere. I can inform you that the temperature of the tropopause lies between -60°C och -80°C and not 0. The relevant quantity you need is the amount of radiation/area hitting the upper boundary of the atmosphere. It can easily be calculated and its annual average amounts to 1/4 of the solar constant or 341W/m2. 102 W/m2 is reflected (the planetary albedo is 30%). The rest, 239W/m2, is re-radiated to space in the form of longwave radiation. It is easily understood that the RESPRESENTATIVE temperature for this re-radiation is approximately 255 K or -18°C. This is because the outgoing terrestrial radiation is absorbed by the greenhouse gases which in turn re-radiate from a lower temperature and so on. The reasoning in this chapter is completely wrong. What happens with an increased concentration of greenhouse gases is that the representative outgoing radiation takes place at a higher level in the atmosphere with the consequence that the ground temperature is increased further. Here you only need to follow the moist/dry-adiabatic temperature profile....

....The entire so called chapter on radiation bears witness of a complete lack of insight into the mechanisms of atmospheric radiation. The comprehensive work that has been carried out during the last 50-70 years is completely neglected. The authors should read Richard Goody's latest edition from 1995 coauthored with Y.L. Yung or Kuo-Nan Liou's from 2002. To me it is incomprehensible how such nonsense can be written by people employed at one of Swedens top-ranking universities, at least that was my attitude before. At least they could have consulted some of the swedish professors of meteorology or some foreign expert on atmospheric radiation in order to avoid the worst crazyness. One can only hope that the students were intelligent enough to see through the bullshit, which is also presented in a very obtrusive and patronising manner...."

It is instructive to see how Bengtsson uses the sloppy and dishonest way of reasoning that I have already disected in the post "What is the greenhouse effect". For some reason, even professors of meteorology prefer the sloppy version. Is it perhaps because they have something to hide? In any case I don't think the students became any wiser from reading Bengtsson's pamphlet.

I have a suggestion for you, Professor Bengtsson. Why don't you also comment on the lapse-rate "bullshit" provided by various physicists in the post "4 different descriptions of the lapse rate"?   

How to freeze water under vacuum

According to G&T:

1.2. What is a physical effect?
 
A physical effect consists of three things:
 
(a) a reproducible experiment in the lab;
(b) an interesting or surprising outcome;
(c) an explanation in terms of a physical theory.

In the video above we see (a) and (b), but what is the explanation?

4 different explanations for the lapse rate

Despite the fact that greenhouse speculations (4) have been with us for at least a century, highly trained physicists seem to be awfully uneducated (irony) on this topic. Read and behold:

1. Serways Principles of Physics ISBN 0-534-49143-X,(kap 16.7 s. 520) 'The atmospheric lapse rate':

" ...We can argue conceptually why the temperature decreases with height.
Imagine a parcel of air moving upward along the slope of a mountain. As
the parcel rises into higher elevations, the pressure on it from the
surrounding air decreases. The pressure difference between the interior
and exterior of the parcel causes the parcel to expand. In doing so, the
parcel is pushing the surrounding air outward, doing work on it. Because
the system is doing work on the environment, the energy in the parcel
decreases. The decreased energy is manifested as a decrease in
temperature..."

2. Erren and Dietze, E&E 2003:

"...Upper layers would
be cooler because the vertical component of the thermal molecular speed
is reduced...."

3. M.N. Berbaran-Santos et al. :

".. The fall of temperature with altitude in the troposhere is due to the fact that air is warmed mainly from the surface of the planet. This fall is, however, smaller than could be expected because convection occurs (up to the tropopause). .."

4. Manabe-Strickler:

".. The observed troposheric lapse rate of temperature is approximately 6.5 deg per km. The explanation for this fact is rather complicated. It is essentially the result of a balance between (a) the stabilizing effect of upward heat transport in moist and dry convection on both small and large scales and (b) the destabilizing effect of radiative transfer... "

The Enigma

We now leave theory for a moment to discuss a little what goes on in the real world. Temperature lapse-rates are often expressed in terms of a decline in temperature as a function of altitude. In reality though, it turns out that pressure is a more convenient vertical coordinate to use. From soundings one finds the following approximate relation between temperature and pressure:

The Theta symbol stands for the ground temperature. This is better confirmed by soundings than the dry adiabatic lapse rate expressed in terms of altitude as

dT/dz = -g/Cp.

It is worthwhile to think for a moment what it means.

Some fuel for thought

It seems as if concepts like temperature and the second law of thermodynamics are difficult to apply on the planetary scale. There are a lot of pitfalls, one or two of which probably most of us has fallen into some time. But there is always opportunity to learn from our mistakes. But physics cannot be determined by the human language. Are there any more physical "hands-on" concepts that we can use instead of abstract notions that might lead to confusion?

Imagine that you go to the beach a warm (25 deg C) day with a backpack full of cold beer. You don't want to drink the beer immediately but rather wait a couple of hours until your friends arrive. From experience you know that in the meantime the beer will warm to ambient temperature unless you do something. There are two options: In the bar at the beach there is a refrigerator which you can use. But next to the beach there is also a two kilometer high mountain and a helicopter standing at your disposal. You could if you want take the backpack in the helicopter, fly to the top of the mountain where the temperature is 8 deg C, leave the beer there and then return to pick it up some hours later. Which is more practical? Which is less energy consuming? I think most of us would find the refrigerator more practical, since going up the mountain requires a lot of work against the gravitational field.

Likewise, the gravity field effectively prevents us from constructing a perpetuum mobile from the temperature difference that is beeing maintained for free between the ground and the top of the mountain. So, what do you then think is the cause of this temperature difference?

Roy again

I will let Roy Spencer summarize some of the points made during the last week by quoting parts of two of his blogposts which can be found here and here.

Roy Spencer on the second law of thermodynamics:

"First of all, the 2nd Law applies to the behavior of whole systems, not to every part within a system, and to all forms of energy involved in the system…not just its temperature. And in the atmosphere, temperature is only one component to the energy content of an air parcel."

Roy Spencer on the state of the earth if there were no greenhouse gases:

"....And what happens when there is a temperature difference in a material? Heat flows by thermal conduction, which would then gradually warm the upper atmosphere to reduce that temperature difference. The process would be slow, because the thermal conductivity of air is quite low. But eventually, the entire atmosphere would reach a constant temperature with height."

Yes, that sounds familiar, isn't it the second law of thermodynamics?

Is the atmosphere an ideal gas, a blackbody or maybe something else?

Mixing or confusing physical concepts can be devastating. In previous posts we have seen examples of  such confusion which appear to be almost semantical. In my view, many misunderstandings could be avoided if

1. The distinctions between dynamic/absolute temperature, kinetic temeparture and empirical temperature were made clear.

2. It was made clear whether the incoming sunlight should be treated as a heat flow or as an energy source.

Moreover, there seems to be a mixing of physical models. On one occasion (radiation) the atmospheric layers are treated as black-bodies, on another occasion (convective overturning, adiabat etc.) they are suddenly transformed into an almost ideal gas. If you follow the links you will discover that their thermodynamic properties, like pressure and heat capacity, differ in a qualitative way. 

However, is there any other way forward? In the end we must have a model that takes into account both radiation and kinetic energy of air molecules. Could such a model be that of a "boson gas"? The idea would be to treat all thermal excitations in the atmosphere, including photons, phonons, molecular momentum and so on as one kind of particle: boson. What would it be like?  

Since the number of bosons is not limited we would have to treat it as a grand canonical ensemble. As a matter of fact, papers have been written on this subject: 

Some excerpts:
 

Can anyone make sense of this?

The hypothesis of Jelbring and the rebuttal by Erren and Dietze

In 2003, Swedish climatologist Hans Jelbring proposed a theory, based mostly on heuristic lines of argument, for explaining the atmospheric lapse rate and its heating impact on the surface. In a way it could be viewed as a modern rendition of the hypothesis of Herapath. The paper, published in E&E, had the title "Greenhouse Effect as a function of Atmospheric Mass". Below is a quote of the central hypothesis:

"In an ideal gas atmosphere, the adiabatic temperature lapse rate has to be –g/cp where cp is the heat capacity of the gas (ref 2 p. 49). Theoretical calculations are well confirmed by observational evidence in the atmosphere of Earth. The adiabatic temperature lapse rate on Earth is thus –9.81/1004 = –0.0098 K/m. As James R. Holton concluded after deriving this result: “Hence, the dry adiabatic lapse rate is approximately constant throughout the lower atmosphere.” The temperature lapse rate in our model atmosphere also has to be –g/cp, since its atmosphere is organized adiabatically."

The paper was followed by a fierce rebuttal  by Hans Erren and Peter Dietze entitled "The Greenhouse Effect should not be redifined" published in the same journal. I will quote parts of the text, hopefully capturing the essence of the message:

"Hans Jelbring titles his paper "The 'Greenhouse effect' as a function of atmospheric mass" though another term would be required as by definition the Greenhouse effect (GE) is a radiative effect, i.e. warming from back-radiation to ground, which is independent of atmospheric mass and adiabatic lapse rate and thus cannot be governed in its magnitude. The GE is from infrared (IR) absorption and thermal re-emission (see chapter "Radiative Forcing" of <http://www.john-daly.com/forcing/moderr.htm>) which occurs independently from the thermodynamic processes that Hans J considers to be the only relevant ones in the troposphere. His suspicion that IPCCs Global Warming (GW) models wrongly consider all the atmospheric energy transport being radiative only, is incorrect. The basic GE modelling copes with the radiative and convective part of the energy fluxes."

It is true that the basic GE modelling takes into account a convective overturning, but the radiative and convective processes are highly interacting, see the post "What is the greenhouse effect". Furthermore:

"In the atmosphere we find a combination of convective lapse (in regions where convection is strong), a gravity lapse plus the radiative lapse. The author seems to deny atmospheric radiation and to consider greenhouse scientists who base their theory on radiative physics as to foolishly believe in conventional radiative models and HITRAN spectra which he considers to be without scientific foundation. He simply redefines the GE as the difference in temperature between the surface
and a non-existent minus 18 degC black body reference shell at an arbitrary level of altitude, resulting from the magnitude of the adiabatic lapse rate. He concludes that this lapse rate is independent of the mass and the temperature of the model atmosphere. He further concludes that the GE expressed by the lapse rate is constant and independent of radiative properties (!) of the constituents. In particular we object his statement that "the atmospheric mass exposed to a gravity field is the cause of the substantial part of GW". Strong doubts arise whether the author has understood the radiative GE at all."

What they mean with "combination of lapses" remains obscure. Notably, they also write:

"If we would assume that no GHGs exist (as they are asserted to be irrelevant) and the Earth had a resting atmosphere which is fully transparent to radiation, the ground would turn to minus 18 degC to get into radiative equilibrium with the incoming solar 240 W/m² - no matter what mass the atmosphere has and to what extent a gravity lapse rate may cause a cooler (than minus 18 °C) upper atmosphere. Upper layers would be cooler because the vertical component of the thermal molecular speed is reduced. This "gravity lapse rate" may be similar to the lapse rate g/Cp that Hans J uses. But it cannot cause a warming (relative to minus 18 degC) of the atmosphere near ground and thus a warming of the ground itself. So the adiabatic lapse rate cannot explain the plus 15 degC ground temperature and thus replace any radiative basic and anthropogenic GE. Any ground warmer than minus 18 DegC would definitely mean a perpetuum mobile permanently producing energy out of gravity. Static air pressure cannot produce permanent heat in an open non-insulated system."

It should be emphasized that the greenhouse hypothesis is not ambiguous on the (average) temperature at any altitude, it is clearly defined for any absorption/emmision parameter. Compare with the wiew of Roy Spencer. 

Roy Spencer defends the Greenhouse Effect

In a blogpost from Roy Spencer published some time ago, he defends the existence of a natural greenhouse effect. The entire post can be read here. I will pick out a few passages that concerns the second law of thermodynamics. Spencer writes the following:

"A second objection has to do with the Second Law of Thermodynamics. It is claimed that since the greenhouse effect depends partly upon cooler upper layers of the atmosphere emitting infrared radiation toward the warmer, lower layers of the atmosphere, that this violates the 2nd Law, which (roughly speaking) says that energy must flow from warmer objects to cooler objects, not the other way around."

There is indeed a formulation of the 2nd law that states the following:

Heat flows spontaneously from higher to lower temperature

He goes on:

"There are different ways to illustrate why this is not a valid objection. First of all, the 2nd Law applies to the behavior of whole systems, not to every part within a system, and to all forms of energy involved in the system…not just its temperature. And in the atmosphere, temperature is only one component to the energy content of an air parcel."

What Spencer wants to say with this is somewhat obscure. The formulation I stated above can be found in standard textbooks on thermodynamics and is pretty straightforward. Furthermore he states that the 2nd law applies to all forms of energy, not just the temperature. First of all, temperature is not a form of energy but relates to energy and entropy by the formula

1/T = dS/dE.

Secondly, the energy he refers to that is not included in the "temperature", does he mean the potential energy? Probably. Well, the potential energy could be included in the heat capacity of the gas, indeed, in statistical mechanics one observes that the heat capacity of an ideal gas in a gravitational field increases to 5/2kT per constituent particle to be compared with the value 3/2kT holding without the field. This accounts for the potential energy of the gas.

Furthermore he writes:

"Secondly, the idea that a cooler atmospheric layer can emit infrared energy toward a warmer atmospheric layer below it seems unphysical to many people. I suppose this is because we would not expect a cold piece of metal to transfer heat into a warm piece of metal. But the processes involved in conductive heat transfer are not the same as in radiative heat transfer. A hot star out in space will still receive, and absorb, radiant energy from a cooler nearby star…even though the NET flow of energy will be in the opposite direction.

In other words, a photon being emitted by the cooler star doesn’t stick its finger out to see how warm the surroundings are before it decides to leave."

This is even more obscure. What precisely is the difference between conductive heat transfer and radiative heat transfer? Is it that when a hot metal plate looses heat to a colder plate it does so because it has first measured the temperature of the colder plate and concluded that it was lower that its own?

We will return to discuss this issue at length later. Stay tuned..

On the temperature profile of an ideal gas under the force of gravity

The discussion concerning the temperature profile of an ideal gas under the force of gravity has a long history. There are many excellent texts on this subject so I will mostly refer the reader to these and just add a few comments of my own.

In an old book on the history of statistical mechanics entitled "The kind of motion we call heat" you can find the following passage:

"...According to Herapath, the force of gravity by itself produces a temperature variation in a vertical column of air, namely a decrease of about 1 F for every 100 yards increase in height above the earth's surface (assuming perfectly dry air); the 'total altitude of the air' would thus be approximately 31 miles, if it terminates when the temperature has dropped to absolute zero.

Herapath's work was refused publication by the Royal Society of London but seems to have had ample publicity through its appearance in several issues of the Annals of Philosophy...."

Clearly, if Herapath is right then the greenhouse hypothesis is wrong, as is explained in the post "What is the greenhouse effect". But is Herapath right? Well, the Royal Society seemed skeptical at the time. There is one problem with his hypothesis that can be expressed quite simply:

The temperature must not become negative

This is so obvious so why do I mention it? Well, if we assume that the ground temperature of the earth is on average 288 K and that the temperature decreases by 9.8 degrees C per kilometer, then the atmosphere must "end" at an altitude of approximately 30 km, otherwise the temperature will become negative.  Today we know that the atmosphere extends to much higher altitudes and that the temperature appears to be stratisfied beginning already at an altitude of 11 km. The stratification must occur at some point independent of any ozone absoption of UV-light and so on.

However, there seems to be something intuitively appealing with the assumption that temperature decreases with height independent of any motions or stirring of the air. In 1985 Coombes and Laue published a paper called "A paradox concerning the temperature distribution of a gas in a gravitational field":

Clearly, we must distinguish between the single particle kinetic energy expectation value and the ensemble average. The fact that the particles with low energy must reside at lower altitudes means that they contribute to lowering the ensemble average of the kinetic energy at these altitudes. Or put in other words, the density decreases according to the barometric formula just as the pressure does, so if the ideal gas law is to be valid the temperature must be uniform in the column.

The problem can also be treated within the context of fluid mechanics under Navier-Stokes equations, yielding some similar but also some slightly different answers.

So where do we go from here, what is the significance of the Coombes-Laue conclusion? We could make an attempt to analyze it from a logical point of view in the following way. Consider the following three definitions of temperature:

1. Absolute Temperature, denoted T

The absolute temperature could be defined using the notion of equilibrium in the following way: Whenever two systems in thermal contact with each other but isolated from the surroundings cease to exchange net heat (energy) they share some common property called temperature. The absolute temperature can be given a number according to the formula 1/T = dS/dE where S is the entropy and E is the internal energy. In order to define the entropy we need to identify the degrees of freedom of the system.

2. Kinetic Temperature, denoted T'

The kinetic temperature we define as the ensemble average of the translational kinetic energy of the molecules. This can only be applied to gases but is not excluded to ideal gases. Allowing the inclusion of water vapour and other gases with extra degrees of freedom does not pose any difficulties.

3. Empirical Temperature, denoted T''

The empirical temperature we define as the reading of some preferred thermometer. This definition differs from the others since it concerns the physical world and not "the world of ideas".

So, what Coombes and Laue showed, as well as many people before them,  was that for a particular statistical ensemble, namely the canonical ensemble of an ideal gas in a gravitational field, we have that T = T'. However, as a matter of fact this is no longer true if you consider the microcanonical ensemble, though the difference in this case may be considered as rather insignificant. In any case, the more relevant question would be the following:

Is, under all circumstances, T = T' = T'' ?

It seems as if the greenhouse hypothesis implies the following answer to the above question:

Under all circumstances we have that T' = T'', but T = T' = T'' holds only if there are no greenhouse gases around. This of course requires that we treat the incoming sunlight as a heat flow regardless of the composition of the atmosphere. It appears as if the controversy concerning the greenhouse effect in relation to the second law of thermodynamics can be formulated as a logical/semantic disagreement of the kind just described.

There are many interesting perceptions of the related problem concerning the atmosphere. The following passage was quoted in the falsification paper of Gerlich and Tscheuschner:

"Some have problems with the energy that is radiated by the greenhouse gases
towards the surface of the Earth (150W=m2 - as shown above) because this energy
flows from a colder body (approx. -40 deg C) to a warmer one (Earth's ground approx.
+15 deg C) apparently violating the second law of thermodynamics. This is
a wrong interpretation, since it ignores the radiation of the Sun (even 6000 K).
With respect to the total balance the second law is obeyed indeed."

There is something very strange about this statement since if we follow the advice given and treat the incoming sunlight as a heat flow then there is no net heat flow between the surface and the atmosphere averaged over a day-night cycle.

What is the greenhouse effect?

If you want to debate the greenhouse effect, a good start is to know what it is. People argue whether there exists such a thing as the greenhouse effect,  however, here we will provide a simplified mathematical formulation that nevertheless captures the essential features. The background information is gathered from Goody and Yung "Atmospheric radiation", Oxford University Press.

The underlying principles are rather simple, the earths surface and the atmospheric layers radiate isotropically according to Stefan-Bolzmanns law but with variable absorption/emissivity. The radiation absorbed is instantly thermalized. Furthermore, the absorption a(z) varies with altitude z according to:

The ground temperature is given by the formula:

Here Fs is a measure of the incoming solar radiation. Finally the lapse rate is given by:

Where H is a height scale. We will now solve these equations numerically for three different values of a0. (H = 1, sigma = 1, Fs = 1 held constant).

The blue line is for a0 = 0, the green line is for a0 = 0.5 and the red line is for a0 = 1. As we can see, by increasing the absorption/emission parameter we heat the surface and cool the upper layers of the atmosphere. Note that for a0 = 0 we have an isothermal atmosphere. In more advanced models the pure radiative equilibrium is modified so that when the lapse rate exceeds a certain critical value convection sets in. These models are called radiative-convective models. A lapse rate neutrally stable to convection is characterized by a constant potential temperature and are often called adiabats. These differ depending on the amount of water vapour present. Of course, the equations presented in the beginning need some further explanation, but we will leave that for now and refer to the litterature. 

See also

Manabe-Strickler

Lindzen

Although we were able to give a mathematical illustration of the greenhouse effect in just a few lines, unfortunately the scientific debate hardly ever reaches this point. Many proponents of the theory don't seem to be willing to communicate it in the way I just did, or they might simply not know what they are talking about.

Usually, successful scientific debates are carried out in the spirit of Leibniz by the parties carefully explaining the axioms, assumptions, approximations and equations underpinning their theory/model. In the greenhouse debate though, neither part seems to be interested in such a discussion. However, from the skeptical point of view the danger of not knowing your target is obvious. You become more succeptible to the sophistry of your opponent, you are more likely to make mistakes and to focus on extraneous details rather than essentials.

Equipped with the equations and their solutions we may now disect some common pseudo descriptions of the greenhouse effect:

1) The greenhouse gases absorb the outgoing terrestrial IR-radiation thereby heating the atmosphere.

Comment: The greenhouse gases do not heat the atmosphere, they change the temperature profile of the atmosphere.

2) By adding greenhouse gases the optical thickness of the atmosphere increases, hence the effective radiating level is pushed to a higher altitude. Since the temperature decreases with increasing altitude, in order to get into equilibrium with the incoming solar radiation the temperature at this new altitude must be that of the blackbody temperature of the earth. The ground temperature is then recovered by following the adiabat.

Comment: This is more to the point but still deceptive. It is true that the red curve crosses the blue curve at a higher altitude than the green curve does, but a lot of information is left out, for example, it is because of the greenhouse effect that the temperature decreases with height in the first place. In essence, the description doesn't explain anything.